Role of Stefan–Maxwell fluxes in the dynamics of concentrated electrolytes
Soft Matter Pub Date: 2018-09-07 DOI: 10.1039/C8SM01222A
Abstract
This theoretical analysis quantifies the effect of coupled ionic fluxes on the charging dynamics of an electrochemical cell. We consider a model cell consisting of a concentrated, binary electrolyte between parallel, blocking electrodes, under a suddenly applied DC voltage. It is assumed that the magnitude of the applied voltage is small compared to the thermal voltage scale, RT/F, where R is the universal gas constant, T is the temperature and F is the Faraday's constant. We employ the Stefan–Maxwell equations to describe the hydrodynamic coupling of ionic fluxes that arise in concentrated electrolytes. These equations inherently account for asymmetry in the mobilities of the ions in the electrolyte. A modified set of Poisson–Nernst–Planck equations, obtained by incorporating Stefan–Maxwell fluxes into the species balances, are formulated and solved in the limit of weak applied voltages. A long-time asymptotic analysis reveals that the electrolyte dynamics occur on two distinct time scales. The first is a faster “RC” time, τRC = κ−1L/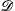
E, where κ−1 is the Debye length, L is the length of the half-cell, and 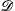E is an effective diffusivity, which characterizes the evolution of charge density at the electrode. The effective diffusivity, 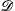E, is a function of the ambi-polar diffusivity of the salt, 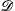a, as well as a cross-diffusivity, 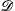+−, of the ions. This time scale also dictates the initial exponential decay of current in the external circuit. At times longer than τRC, the external current again decays exponentially on a slower, diffusive time scale, τD ∼ L2/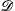a, where 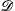a is the ambi-polar diffusivity of the salt. This diffusive time scale is due to the unequal ion mobilities that result in a non-uniform bulk concentration of the salt during the charging process. Finally, we propose an approach by which our theory may be used to measure the cross-diffusivity in concentrated electrolytes.
Recommended Literature
- [1] An efficient method to achieve a balanced open circuit voltage and short circuit current density in polymer solar cells†
- [2] Synthesis of aminoboronic acid derivatives: an update on recent advances†
- [3] Cation-responsive cavity expansion of valinomycin revealed by cryogenic ion trap infrared spectroscopy†
- [4] Seamless lamination of a concave–convex architecture with single-layer graphene†
- [5] Correction: The first computational study for the oxidative aromatization of pyrazolines and 1,4-dihydropyridines using 1,2,4-triazolinediones: an anomeric-based oxidation
- [6] Mechanically induced tilt in smectic-A elastomers
- [7] Probing Lewis acidity of Y(BH4)3via its reactions with MBH4 (M = Li, Na, K, NMe4)†‡
- [8] Inside back cover
- [9] Unexpected side reactions of imidazolium-based ionic liquids in the base-catalysed Baylis–Hillman reaction†
- [10] Nonlinear chiral rheology of phospholipid monolayers†
Journal Name：Soft Matter
Research Products
-
CAS no.: 14941-53-8
-
CAS no.: 131896-42-9
