Structural universality in disordered packings with size and shape polydispersity†
Soft Matter Pub Date: 2020-04-08 DOI: 10.1039/D0SM00110D
Abstract
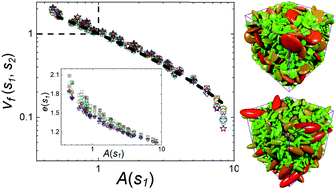
We numerically investigate disordered jammed packings with both size and shape polydispersity, using frictionless superellipsoidal particles. We implement the set Voronoi tessellation technique to evaluate the local specific volume, i.e., the ratio of cell volume over particle volume, for each individual particle. We focus on the average structural properties for different types of particles binned by their sizes and shapes. We generalize the basic observation that the larger particles are locally packed more densely than the smaller ones in a polydisperse-sized packing into systems with coupled particle shape dispersity. For this purpose, we define the normalized free volume vf to measure the local compactness of a particle and study its dependency on the normalized particle size A. The definition of vf relies on the calibrated monodisperse specific volume for a certain particle shape. For packings with shape dispersity, we apply the previously introduced concept of equivalent diameter for a non-spherical particle to define A properly. We consider three systems: (A) linear superposition states of mixed-shape packings, (B) merely polydisperse-sized packings, and (C) packings with coupled size and shape polydispersity. For (A), the packing is simply considered as a mixture of different subsystems corresponding to monodisperse packings for different shape components, leading to A = 1, and vf = 1 by definition. We propose a concise model to estimate the shape-dependent factor αc, which defines the equivalent diameter for a certain particle. For (B), vf collapses as a function of A, independent of specific particle shape and size polydispersity. Such structural universality is further validated by a mean-field approximation. For (C), we find that the master curve vf(A) is preserved when particles possess similar αc in a packing. Otherwise, the dispersity of αc among different particles causes the deviation from vf(A). These findings show that a polydisperse packing can be estimated as the combination of various building blocks, i.e., bin components, with a universal relation vf(A).
Recommended Literature
- [1] The urea cycle of rat white adipose tissue
- [2] Unique [core+two] structure and optical property of a dodeca-ligated undecagold cluster: critical contribution of the exo gold atoms to the electronic structure†
- [3] The crystal and molecular structure of 1,6:8,13-butane-diylidene[14]annulene
- [4] Contribution of convection and diffusion to the cascade reaction kinetics of β-galactosidase/glucose oxidase confined in a microchannel†
- [5] Interfacial TiN bonding of a g-C3N4/TiH1.92 type-II heterojunction photocatalyst significantly enhanced photocatalytic hydrogen evolution from water splitting†
- [6] Interpretation of the pressure-induced Raman frequency shift of the ν1 stretching bands of CH4 and N2 within CH4–CO2, N2–CO2 and CH4–N2 binary mixtures†
- [7] Excited-state intramolecular proton transfer and conformational relaxation in 4′-N,N-dimethylamino-3-hydroxyflavone doped in acetonitrile crystals†
- [8] Highly focused high-frequency travelling surface acoustic waves (SAW) for rapid single-particle sorting†
- [9] Highly sensitive pH dependent acetone sensor based on ultrananocrystalline diamond materials at room temperature
- [10] XXIV.—On narcotine, cotarnine, and hydrocotarnine. Part V. On new cotarnine derivatives and on nor-opianic acid

Journal Name:Soft Matter
Research Products
-
CAS no.: 103646-29-3
-
CAS no.: 179111-05-8









